Wolfram|Alpha provides broad functionality for partial fraction decomposition. Given any rational function, it can compute an equivalent sum of fractions whose denominators are irreducible. It can also utilize this process while determining asymptotes and evaluating integrals, and in many other contexts including control theory.
Online Partial Fraction Decomposition Calculator
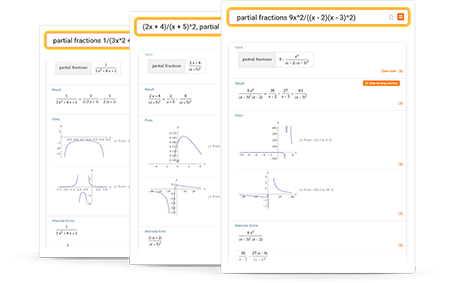
Partial fraction decomposition using Wolfram|Alpha
A general tool for partial fraction decomposition
Learn more about:
Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about applying partial fraction decomposition.
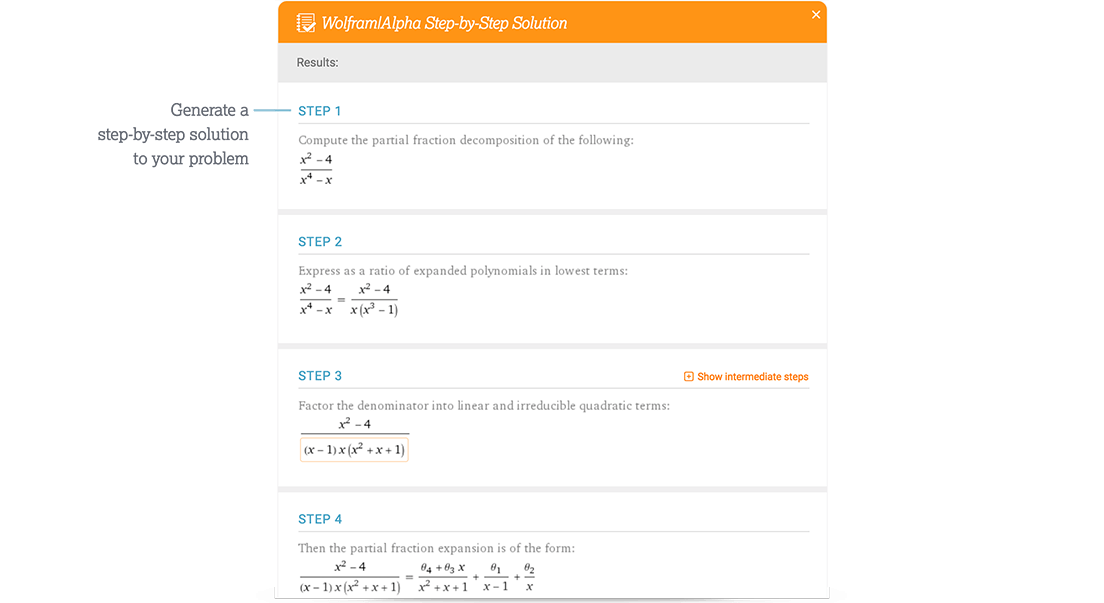
Access Step-by-Step Solutions
Get immediate feedback and guidance with step-by-step solutions
Learn more about:
What is partial fraction decomposition?
Partial fraction decomposition is a useful process when taking antiderivatives of many rational functions.
It involves factoring the denominators of rational functions and then generating a sum of fractions whose denominators are the factors of the original denominator. Bézout's identity suggests that numerators exist such that the sum of these fractions equals the original rational function. The process of partial fraction decomposition is the process of finding such numerators. The result is an expression that can be more easily integrated or antidifferentiated.
There are various methods of partial fraction decomposition. One method is the method of equating coefficients. This involves matching terms with equivalent powers and performing algebra to find missing coefficients. It is a common method, and one based on the method of undetermined coefficients. Alternative methods include one based on Lagrange interpolation, another based on residues and more.
The study of partial fraction decomposition is important to calculus, differential equations and other areas, and is also known as partial fraction expansion.