Wolfram|Alpha is a great tool for finding discontinuities of a function. It also shows the step-by-step solution, plots of the function and the domain and range.
Online Discontinuity Calculator
Find discontinuities of a function with Wolfram|Alpha
More than just an online tool to explore the continuity of functions
Learn more about:
Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for discontinuities.
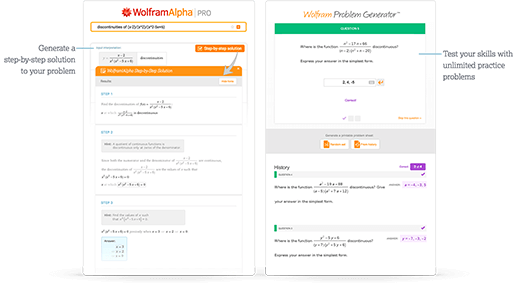
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Learn more about:
What are discontinuities?
A discontinuity is a point at which a mathematical function is not continuous.
Given a one-variable, real-valued function y = f x, there are many discontinuities that can occur. The simplest type is called a removable discontinuity. Informally, the graph has a "hole" that can be "plugged." For example, f x = x-1x2-1 has a discontinuity at x = 1 (where the denominator vanishes), but a look at the plot shows that it can be filled with a value of 12 . Put formally, a real-valued univariate function y = f x is said to have a removable discontinuity at a point x0 in its domain provided that both f x0 and limxx0f x = L < ∞ exist.
Another type of discontinuity is referred to as a jump discontinuity. Informally, the function approaches different limits from either side of the discontinuity. For example, the floor function f x = x has jump discontinuities at the integers; at x = 2, it jumps from 1 (the limit approaching from the left) to 2 (the limit approaching from the right). A real-valued univariate function y = f x has a jump discontinuity at a point x0 in its domain provided that limxx0-f x = L1 and limxx0+f x = L2 both exist, are finite and that L1≠L2.
A third type is an infinite discontinuity. A real-valued univariate function y = f x is said to have an infinite discontinuity at a point x0 in its domain provided that either (or both) of the lower or upper limits of f goes to positive or negative infinity as x tends to x0. For example, f x = x-1x2-1 (from our "removable discontinuity" example) has an infinite discontinuity at x = −1. To the right of -1, the graph goes to ∞, and to the left it goes to -∞.
There are further features that distinguish in finer ways between various discontinuity types. They involve, for example, rate of growth of infinite discontinuities, existence of integrals that go through the point(s) of discontinuity, behavior of the function near the discontinuity if extended to complex values, existence of Fourier transforms and more.