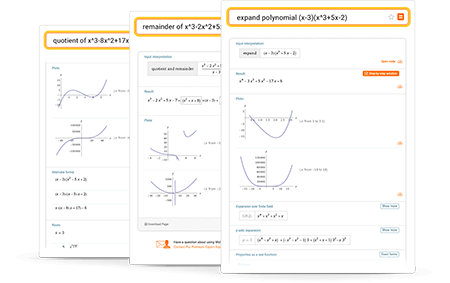
Wolfram|Alpha is a great tool for factoring, expanding or simplifying polynomials. It also multiplies, divides and finds the greatest common divisors of pairs of polynomials; determines values of polynomial roots; plots polynomials; finds partial fraction decompositions; and more.
Online Factoring Calculator
Factor, expand or simplify polynomials with Wolfram|Alpha
More than just an online factoring calculator
Learn more about:
Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about factoring.
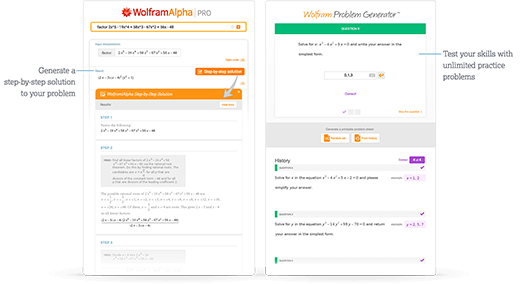
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Learn more about:
What is factoring?
A polynomial with rational coefficients can sometimes be written as a product of lower-degree polynomials that also have rational coefficients. In such cases, the polynomial is said to "factor over the rationals." Factoring is a useful way to find rational roots (which correspond to linear factors) and simple roots involving square roots of integers (which correspond to quadratic factors).
Polynomials with rational coefficients always have as many roots, in the complex plane, as their degree; however, these roots are often not rational numbers. In such cases, the polynomial will not factor into linear polynomials.
Rational functions are quotients of polynomials. Like polynomials, rational functions play a very important role in mathematics and the sciences. Just as with rational numbers, rational functions are usually expressed in "lowest terms." For a given numerator and denominator pair, this involves finding their greatest common divisor polynomial and removing it from both the numerator and denominator.