Wolfram|Alpha computes both one-dimensional and multivariate limits with great ease. Determine the limiting values of various functions, and explore the visualizations of functions at their limit points with Wolfram|Alpha.
Online Limit Calculator
All you could want to know about limits from Wolfram|Alpha
A handy tool for solving limit problems

Learn more about:
Tips for entering queries
Use plain English or common mathematical syntax to enter your queries. For specifying a limit argument x and point of approach a, type "x -> a". For a directional limit, use either the + or – sign, or plain English, such as "left," "above," "right" or "below."
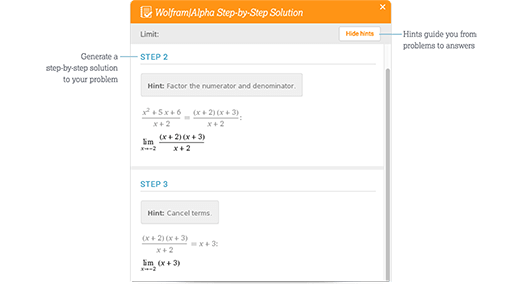
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions
Learn more about:
What are limits?
Limits, a foundational tool in calculus, are used to determine whether a function or sequence approaches a fixed value as its argument or index approaches a given point.
Limits can be defined for discrete sequences, functions of one or more real-valued arguments or complex-valued functions. For a sequence xn indexed on the natural number set n ∈ N, the limit L is said to exist if, as n → ∞, the value of the elements of xn get arbitrarily close to L.
A real-valued function f x is said to have a limit L if, as its argument x is taken arbitrarily close to x0, its value can be made arbitrarily close to L. Formally defined, a function f x has a finite limit L = limxx0f x at point x0 if, for all ε > 0 , there exists δ > 0 such that f x - L < ε whenever x - x0 < δ. This definition can be further extended for L or x0 being taken to infinity and to multivariate and complex functions.
For functions of one real-valued variable, the limit point x0 can be approached from either the right/above (denoted limxx0+f x) or the left/below (denoted limxx0-f x). In principle, these can result in different values, and a limit is said to exist if and only if the limits from both above and below are equal: limxx0f x = limxx0+f x = limxx0-f x. For multivariate or complex-valued functions, an infinite number of ways to approach a limit point exist, and so these functions must pass more stringent criteria in order for a unique limit value to exist.
In addition to the formal definition, there are other methods that aid in the computation of limits. For example, algebraic simplification can be used to eliminate rational singularities that appear in both the numerator and denominator, and l'Hôpital's rule is used when encountering indeterminate limits, which appear in the form of an irreducible 00 or ∞∞ .
How Wolfram|Alpha solves limit problems
Wolfram|Alpha calls Mathematica's built-in function Limit to perform the computation, which doesn't necessarily perform the computation the same as a human would. Usually, the Limit function uses powerful, general algorithms that often involve very sophisticated math.
In addition to this, understanding how a human would take limits and reproducing human-readable steps is critical, and thanks to our step-by-step functionality, Wolfram|Alpha can also demonstrate the techniques that a person would use to compute limits. Wolfram|Alpha employs such methods as l'Hôpital's rule, the squeeze theorem, the composition of limits and the algebra of limits to show in an understandable manner how to compute limits.