Wolfram|Alpha can apply the quadratic formula to solve equations coercible into the form ax2 + bx + c = 0. In doing so, Wolfram|Alpha finds both the real and complex roots of these equations. It can also utilize other methods helpful to solving quadratic equations, such as completing the square, factoring and graphing.
Online Quadratic Formula Calculator
Apply the quadratic formula using Wolfram|Alpha
A useful tool for finding the solutions to quadratic equations

Learn more about:
Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask about finding roots of quadratic equations.
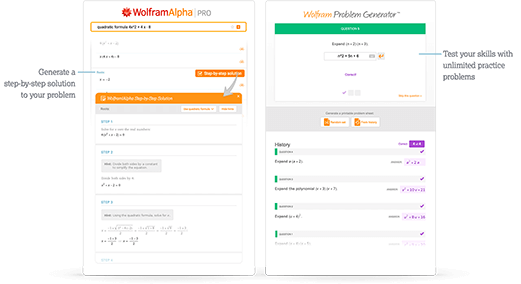
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Learn more about:
What are quadratic equations, and what is the quadratic formula?
A quadratic is a polynomial of degree two.
Quadratic equations form parabolas when graphed, and have a wide variety of applications across many disciplines. In physics, for example, they are used to model the trajectory of masses falling with the acceleration due to gravity.
Situations arise frequently in algebra when it is necessary to find the values at which a quadratic is zero. In other words, it is necessary to find the zeros or roots of a quadratic, or the solutions to the quadratic equation. Relating to the example of physics, these zeros, or roots, are the points at which a thrown ball departs from and returns to ground level.
One common method of solving quadratic equations involves expanding the equation into the form ax2 + bx + c = 0 and substituting the a, b and c coefficients into a formula known as the quadratic formula. This formula, x = -b ± b2 - 4ac2a , determines the one or two solutions to any given quadratic. Sometimes, one or both solutions will be complex valued.
Discovered in ancient times, the quadratic formula has accumulated various derivations, proofs and intuitions explaining it over the years since its conception. Some involve geometric approaches. Others involve analysis of extrema. There are also many others. Those listed and more are often topics of study for students learning the process of solving quadratic equations and finding roots of equations in general.
Alternative methods for solving quadratic equations do exist. Completing the square, factoring and graphing are some of many, and they have use cases—but because the quadratic formula is a generally fast and dependable means of solving quadratic equations, it is frequently chosen over the other methods.