Wolfram|Alpha is the perfect resource to use for computing determinants of matrices. It can also calculate matrix products, rank, nullity, row reduction, diagonalization, eigenvalues, eigenvectors and much more.
Online Determinant Calculator
Take the determinant of matrices with Wolfram|Alpha
More than just an online determinant calculator

Learn more about:
Tips for entering queries
Use plain English or common mathematical syntax to enter your queries. To enter a matrix, separate elements with commas and rows with curly braces, brackets or parentheses.
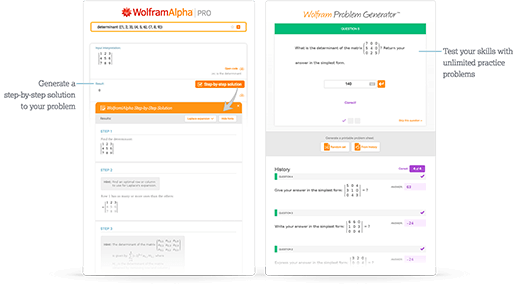
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Learn more about:
Knowledgebase about determinants
A determinant is a property of a square matrix.
The value of the determinant has many implications for the matrix. A determinant of 0 implies that the matrix is singular, and thus not invertible. A system of linear equations can be solved by creating a matrix out of the coefficients and taking the determinant; this method is called Cramer's rule, and can only be used when the determinant is not equal to 0. Geometrically, the determinant represents the signed area of the parallelogram formed by the column vectors taken as Cartesian coordinates.
There are many methods used for computing the determinant. Some matrices, such as diagonal or triangular matrices, can have their determinants computed by taking the product of the elements on the main diagonal. For a 2-by-2 matrix, the determinant is calculated by subtracting the reverse diagonal from the main diagonal, which is known as the Leibniz formula. The determinant of the product of matrices is equal to the product of determinants of those matrices, so it may be beneficial to decompose a matrix into simpler matrices, calculate the individual determinants, then multiply the results. Some useful decomposition methods include QR, LU and Cholesky decomposition. For more complicated matrices, the Laplace formula (cofactor expansion), Gaussian elimination or other algorithms must be used to calculate the determinant.