Wolfram|Alpha is a great calculator for first, second and third derivatives; derivatives at a point; and partial derivatives. Learn what derivatives are and how Wolfram|Alpha calculates them.
Online Derivative Calculator
Solve derivatives with Wolfram|Alpha
More than just an online derivative solver
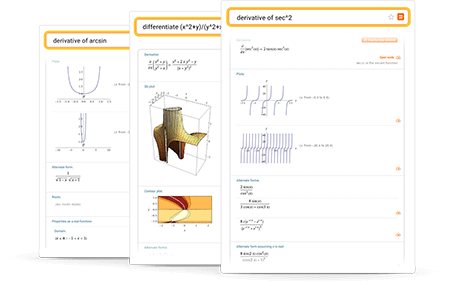
Learn more about:
Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for a derivative.
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
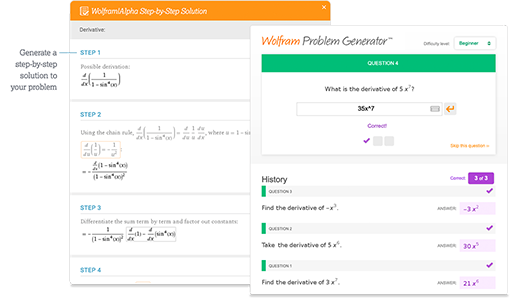
Learn more about:
What are derivatives?
The derivative is an important tool in calculus that represents an infinitesimal change in a function with respect to one of its variables.
Given a function , there are many ways to denote the derivative of with respect to . The most common ways are and . When a derivative is taken times, the notation or is used. These are called higher-order derivatives. Note for second-order derivatives, the notation is often used.
At a point , the derivative is defined to be . This limit is not guaranteed to exist, but if it does, is said to be differentiable at . Geometrically speaking, is the slope of the tangent line of at .
As an example, if , then and then we can compute : . The derivative is a powerful tool with many applications. For example, it is used to find local/global extrema, find inflection points, solve optimization problems and describe the motion of objects.
How Wolfram|Alpha calculates derivatives
Wolfram|Alpha calls Wolfram Languages's D function, which uses a table of identities much larger than one would find in a standard calculus textbook. It uses well-known rules such as the linearity of the derivative, product rule, power rule, chain rule and so on. Additionally, D uses lesser-known rules to calculate the derivative of a wide array of special functions. For higher-order derivatives, certain rules, like the general Leibniz product rule, can speed up calculations.